
En el post de esta semana vamos a continuar la serie temática «Diseño de Instalaciones de Protección Contra Incendios (PCI)» dedicada a conocer los principios básicos que se deben aplicar en el diseño de una instalación de protección contra incendios (PCI). Como ya sabéis, para esta serie temática cuenta con la colaboración de Adolfo Sahuquillo.
Ecuación de Bernoulli
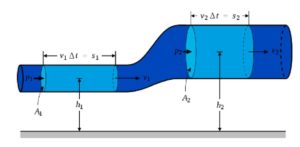
Evaluemos los cambios energéticos que ocurren en la porción de fluido señalada en color amarillo, cuando se desplaza a lo largo de la tubería. En la figura, se señala la situación inicial y se compara la situación final después de un tiempo Dt. Durante dicho intervalo de tiempo, la cara posterior S2 se ha desplazado v2 Dt y la cara anterior S1 del elemento de fluido se ha desplazado v1Dt hacia la derecha.
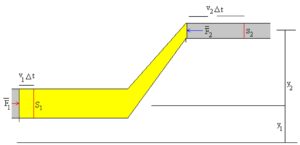
El elemento de masa Dm se puede expresar como Dm=r S2v2Dt=r S1v1Dt= r DV
Comparando la situación inicial en el instante t y la situación final en el instante t+Dt. Observamos que el elemento Dm incrementa su altura, desde la altura y1 a la altura y2
- La variación de energía potencial es DEp=Dm·gy2-Dm·gy1=r DV·(y2-y1)g
El elemento Dm cambia su velocidad de v1 a v2,
- La variación de energía cinética es
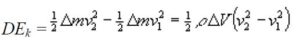
El resto del fluido ejerce fuerzas debidas a la presión sobre la porción de fluido considerado, sobre su cara anterior y sobre su cara posterior F1=p1S1 y F2=p2S2.
La fuerza F1 se desplaza Dx1=v1Dt. La fuerza y el desplazamiento son del mismo signo
La fuerza F2 se desplaza Dx2=v2 Dt. La fuerza y el desplazamiento son de signos contrarios.
- El trabajo de las fuerzas exteriores es Wext=F1 Dx1- F2 Dx2=(p1-p2) DV
El teorema del trabajo-energía nos dice que el trabajo de las fuerzas exteriores que actúan sobre un sistema de partículas modifica la energía del sistema de partículas, es decir, la suma de las variaciones de la energía cinética y la energía potencial del sistema de partículas
Wext=Ef-Ei=(Ek+Ep)f-(Ek+Ep)i=DEk+DEp
Simplificando el término DV y reordenando los términos obtenemos la ecuación de Bernoulli.
![]()
Efecto Venturi
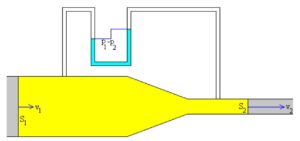
Cuando el desnivel es cero, la tubería es horizontal. Tenemos entonces, el denominado tubo de Venturi, cuya aplicación práctica es la medida de la velocidad del fluido en una tubería. El manómetro mide la diferencia de presión entre las dos ramas de la tubería.
La ecuación de continuidad se escribe
v1S1=v2S2
Que nos dice que la velocidad del fluido en el tramo de la tubería que tiene menor sección es mayor que la velocidad del fluido en el tramo que tiene mayor sección. Si S1>S2, se concluye que v1<v2.
La en la ecuación de Bernoulli con y1=y2
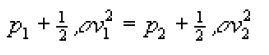
Como la velocidad en el tramo de menor sección es mayor, la presión en dicho tramo es menor.
Si v1<v2 se concluye que p1>p2 El líquido manométrico desciende por el lado izquierdo y asciende por el derecho
Podemos obtener las velocidades v1 y v2 en cada tramo de la tubería a partir de la lectura de la diferencia de presión p1-p2 en el manómetro.
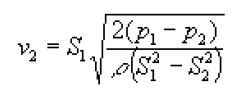
Ejemplo:
Supongamos que introducimos los siguientes datos en el programa interactivo:
- Radio del tramo izquierdo de la tubería, 20 cm.
- Radio del tramo derecho de la tubería, está fijado en el programa interactivo y vale 5 cm.
- Velocidad del fluido en el tramo izquierdo, 10 cm/s
- Desnivel ente ambos tramos, 0.0 cm
Si la medida de la diferencia de presión en el manómetro es de 1275 Pa, determinar la velocidad del fluido en ambos tramos de la tubería.
Los datos son:
![]()
Introduciendo estos datos en la fórmula nos da v2=1.6 m/s. Calculamos v1 a partir de la ecuación de continuidad v1=0.1 m/s ó 10 cm/s que es el dato introducido previamente en el programa.
Pérdidas de Carga:
- Las pérdidas de carga se identifican con la pérdida de energía de un flujo hidráulico a lo largo de una conducción, por efecto del rozamiento
- Conforme a la ecuación de Bernoulli:
El principio de Bernoulli, también denominado ecuación de Bernoulli o Trinomio de Bernoulli, describe el comportamiento de un fluido moviéndose a lo largo de una línea de corriente. Fue expuesto por Daniel Bernoulli en su obra Hidrodinámica (1738) y expresa que en un fluido ideal (sin viscosidad ni rozamiento) en régimen de circulación por un conducto cerrado, la energía que posee el fluido permanece constante a lo largo de su recorrido. La energía de un fluido en cualquier momento consta de tres componentes:
1. Cinético: es la energía debida a la velocidad que posea el fluido.
2. Potencial gravitacional: es la energía debido a la altitud que un fluido posea.
3. Energía de flujo: es la energía que un fluido contiene debido a la presión que posee.
La siguiente ecuación conocida como «Ecuación de Bernoulli» (Trinomio de Bernoulli) consta de estos mismos términos.
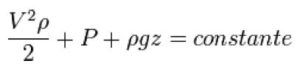
donde:
V = velocidad del fluido en la sección considerada.
z = altura en la dirección de la gravedad desde una cota de referencia.
P = presión a lo largo de la línea de corriente.
ρ= densidad del fluido.
Para aplicar la ecuación se deben realizar los siguientes supuestos:
- Viscosidad (fricción interna) = 0 Es decir, se considera que la línea de corriente sobre la cual se aplica se encuentra en una zona ‘no viscosa’ del fluido.
- Caudal constante
- Fluido incompresible, donde ρes constante.
- La ecuación se aplica a lo largo de una línea de corriente.
Aunque el nombre de la ecuación se debe a Bernoulli, la forma arriba expuesta fue presentada en primer lugar por Leonhard Euler.
Un ejemplo de aplicación del principio lo encontramos en el flujo de agua en tubería.
Características y consecuencias
Cada uno de los términos de esta ecuación tiene unidades de longitud, y a la vez representan formas distintas de energía; en hidráulica es común expresar la energía en términos de longitud, y se habla de altura o cabezal. Así en la ecuación de Bernoulli los términos suelen llamarse alturas o cabezales de velocidad, de presión y cabezal hidráulico, del inglés hydraulic head; el término z se suele agrupar con P / γ para dar lugar a la llamada altura piezométrica o también carga piezométrica.

También podemos reescribir este principio en forma de suma de presiones multiplicando toda la ecuación por γ, de esta forma el término relativo a la velocidad se llamará presión dinámica, los términos de presión y altura se agrupan en la presión estática.
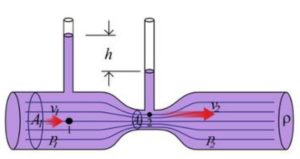
Esquema del efecto Venturi
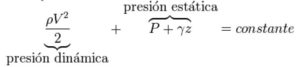
o escrita de otra manera más sencilla:
q + p = p0
donde
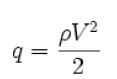
p = P + γz
p0 es una constante.
Igualmente podemos escribir la misma ecuación como la suma de la energía cinética, la energía de flujo y la energía potencial gravitatoria por unidad de masa:
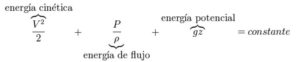
Así el principio de bernoulli puede ser visto como otra forma de la ley de la conservación de la energía, es decir, en una línea de corriente cada tipo de energía puede subir o disminuir en virtud de la disminución o el aumento de las otras dos.
Esta ecuación permite explicar fenómenos como el efecto Venturi, ya que la aceleración de cualquier fluido en un camino equipotencial (con igual energía potencial) implicaría una disminución de la presión. Gracias a este efecto observamos que las cosas ligeras muchas veces tienden a salirse de un automóvil en movimiento cuando se abren las ventanas, ya que la presión del aire es menor fuera del auto ya que está en movimiento respecto a aquél que se encuentra dentro del auto, donde la presión es necesariamente mayor; pero en forma aparentemente contradictoria el aire entra al carro, pero esto ocurre por fenómenos de turbulencia y capa límite.
Ecuación de Bernoulli y la Primera Ley de la Termodinámica
De la primera ley de la termodinámica se puede concluir una ecuación estéticamente parecida a la ecuación de Bernouilli anteriormente señalada, pero conceptualmente distinta. La diferencia fundamental yace en los límites de funcionamiento y en la formulación de cada fórmula. La ecuación de Bernoulli es un balance de fuerzas sobre una partícula de fluido que se mueve a través de una linea de corriente, mientras que la primera ley de la termodinámica consiste en un balance de energía entre los límites de un volumen de control dado, por lo cual es más general ya que permite expresar los intercambios energéticos a lo largo de una corriente de fluido, como lo son las pérdidas por fricción que restan energía, y las bombas o ventiladores que suman energía al fluido. La forma general de esta, llamémosla, «forma energética de la ecuación de Bernoulli» es:
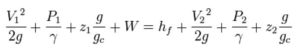
donde:
- γ es el peso específico (γ = ρg).
- W es una medida de la energía que se le suministra al fluido.
- hf es una medida de la energía empleada en vencer las fuerzas de fricción a través del recorrido del fluido.
- Los subíndices 1 y 2 indican si los valores está dados para el comienzo o el final del volumen de control respectivamente.
- g = 9,81 m/s2 y gc = 1 kg·m/(N·s2)
Según la expresión anterior de Bernoulli, obtenemos:
Hm = Hg + Pc + 10 x (Pi ・Pa)/φ, donde;
- Hm (mcda): Presió manomérica.
- Pc (mcda): Pédidas de rozamiento (Hazen Williams).
- Hg (mcda): Pédidas por altura.
- 10 x (Pi ・Pa)/φ (mcda): Diferencial de presión atmosférica.
La expresión de Hazen Williams es como sigue:

- Q: Caudal (lts/min).
- C: Constante de Hazen Williams.
- d: Diámetro (mm).
- L: Longitud de tubo (mts).
Valores de la Constante de HAZEN-WILLIAMS «C», para diferentes tipos de Tuberías.
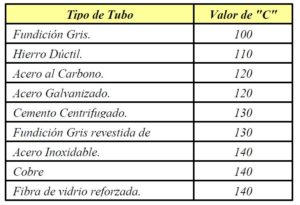
Nota: Cuando se trate de una instalación antigua (a partir de 10 años), tomaremos como valor C = 100 (debido a la rugosidad por las partículas adheridas a la pared del tubo).
Ejemplos de Hidráulica Básica
Los conceptos anteriores, es para tener un patrón de donde obtener los datos, ahora en los ejemplos se establecerá como obtener los resultados de manera más directa;
Nota: Podréis observar, que la mayoría de los conceptos se obtienen con el teorema de Bernoulli.
Ejemplo 1:
Tenemos una tubería de Acero de 6″ SCH-40 por donde trasladamos un caudal de 5.000 lpm, la línea tiene 250 ml de longitud, la presión en su origen es de 8 bar ¿qué presión real tenemos en la salida?
Si aplicamos la fórmula de hacen Williams, obtendremos las pérdidas por rozamiento en la tubería, como valor «C», utilizaremos 120 ya que se trata de tubería de acero al carbono.
Una tubería de 6″ SCH-40, tiene un diámetro internos de 154,08 mm (Se debe utilizar siempre el valor del diámetro interior).
P (bar) = 3,3 bar (Pérdidas de presión).
Presión a salida de red = 8 bar – 3,3 bar = 4,7 bar.
Ejemplo 2:
¿Cuál es la velocidad del agua del Ejemplo 1?
V (m/s) = (21,22 x Q lpm)/di ² (mm);
V (m/s) = (21,22 x 5.000 lpm) / (154,08 mm)²;
V (m/s) = 4,47 m/s.
Director Regional ASHES FIRE CONSULTING